Symmetry 1
상위 디렉토리 - Kalmar CTF 2024
This is one of ransomware type challenges.
The whole code flow of the program is similar to a block cipher, and all information for decrypt is contained in data.txt.
So all I have to do is analyze the encrypt algorithm and then just decrypt it.
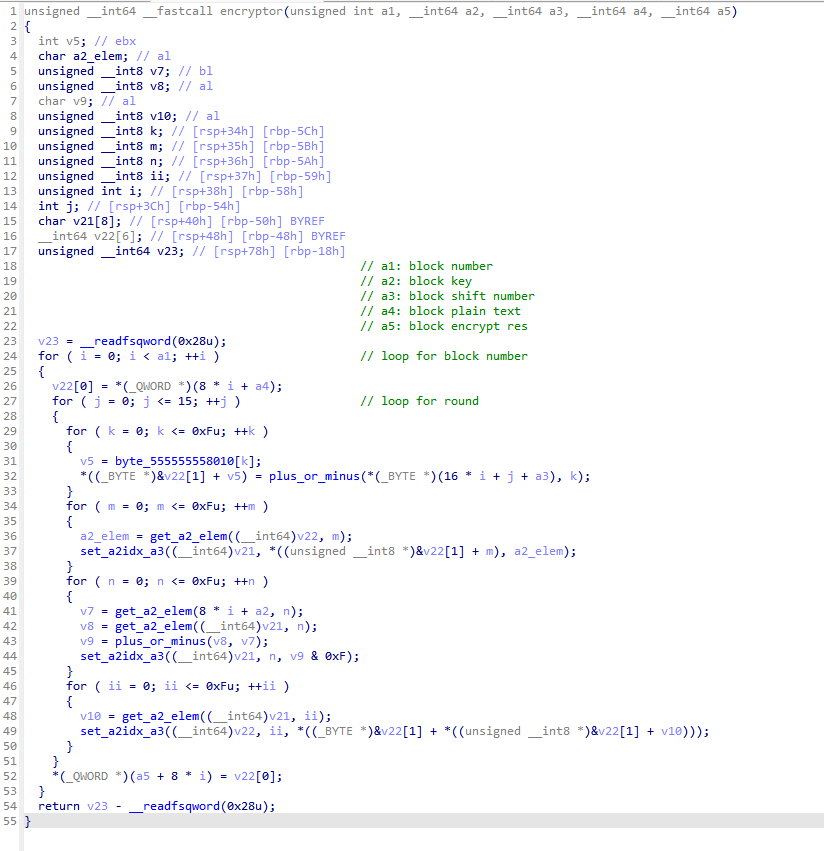
The encryption process is very intuitive, and the inverse calculation is also very simple, except for the plus_or_minus() function.
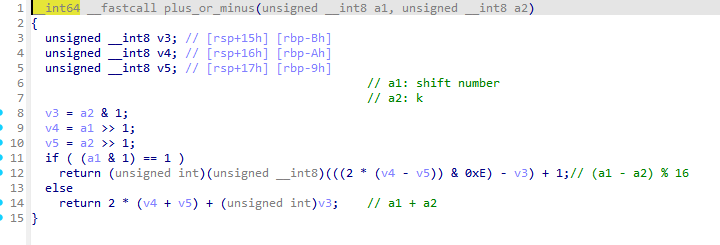
If a1 is an odd number, this function returns (a1 - a2) % 16 . Otherwise, it returns a1 + a2 .
In the inverse calculation, we know the return value and a2. And we know the following very obvious law. “odd + odd = even”, “odd - odd = even”, “even + even = even”, “even - even = even”, “odd + even = odd”, “odd - even = odd”, “even - odd = odd”.
With the above laws, it is not hard to predict whether that a1 is odd or even. After identifying whether a1 is odd or even, the inverse calculation is very, very easy.
Below is the full exploit code, including the implementation(encryption) code and the decryption code.
exploit code
keys=[[2, 3, 3, 5, 3, 3, 1, 4, 1, 1, 3, 3, 1, 2, 2, 0], [5, 1, 5, 4, 7, 3, 2, 0, 0, 1, 7, 1, 0, 6, 2, 7], [2, 6, 6, 0, 5, 6, 5, 1, 6, 4, 7, 1, 1, 7, 3, 1], [4, 3, 0, 5, 2, 0, 4, 2, 7, 7, 7, 1, 1, 1, 7, 5], [1, 0, 0, 0, 4, 5, 3, 6, 3, 4, 7, 6, 4, 0, 1, 2], [5, 5, 7, 1, 3, 1, 7, 6, 6, 3, 1, 1, 2, 4, 6, 7], [2, 6, 2, 4, 1, 6, 0, 3, 7, 0, 6, 3, 0, 6, 7, 3]]
shifts=[[0, 1, 3, 5, 0, 1, 1, 0, 0, 1, 3, 5, 0, 1, 1, 0], [0, 1, 3, 5, 0, 1, 1, 0, 0, 1, 3, 5, 0, 1, 1, 0], [0, 1, 3, 5, 0, 1, 1, 0, 0, 1, 3, 5, 0, 1, 1, 0], [0, 1, 3, 5, 0, 1, 1, 0, 0, 1, 3, 5, 0, 1, 1, 0], [0, 1, 3, 5, 0, 1, 1, 0, 0, 1, 3, 5, 0, 1, 1, 0], [0, 1, 3, 5, 0, 1, 1, 0, 0, 1, 3, 5, 0, 1, 1, 0], [0, 1, 3, 5, 0, 1, 1, 0, 0, 1, 3, 5, 0, 1, 1, 0]]
ciphertexts=[[8, 12, 10, 7, 2, 6, 3, 2, 14, 1, 8, 4, 2, 12, 9, 15], [10, 13, 5, 2, 13, 12, 11, 5, 14, 5, 3, 12, 4, 11, 0, 9], [10, 4, 0, 3, 9, 13, 13, 2, 2, 1, 0, 4, 3, 15, 11, 12], [7, 13, 1, 13, 9, 9, 9, 10, 9, 12, 3, 0, 1, 10, 7, 12], [13, 3, 10, 6, 9, 9, 2, 13, 1, 10, 13, 0, 4, 2, 1, 0], [6, 2, 2, 2, 15, 9, 12, 4, 7, 6, 2, 15, 1, 10, 14, 7], [10, 12, 6, 14, 14, 2, 14, 12, 15, 0, 15, 0, 8, 9, 4, 2]]
byte_4010 = [0x09, 0x0A, 0x08, 0x01, 0x0E, 0x03, 0x07, 0x0F, 0x0B, 0x0C, 0x02, 0x00, 0x04, 0x05, 0x06, 0x0D]
def plus_or_minus(shift_num, k):
if shift_num & 1 == 0:
return shift_num + k
v3 = k & 1
res = 2 * ((shift_num >> 1) - (k >> 1))
res &= 0xE
res -= v3
res += 1
return res
def rev_pm(res, k):
if res & 1 == 0:
a = k & 1
else:
a = 1 - (k & 1)
if a == 0:
return (res - k) % 16
else:
return (res + k) % 16
def round(plain_text, b):
v22_1 = []
v21 = []
for i in range(16):
v22_1.append(0)
for i in range(16):
v21.append(0)
for i in range(16):
for j in range(16):
v22_1[byte_4010[j]] = plus_or_minus(shifts[b][i], j)
for j in range(16):
v21[v22_1[j]] = plain_text[j]
print(v21)
for j in range(16):
tmp1 = keys[b][j]
tmp2 = v21[j]
tmp_res = plus_or_minus(tmp2, tmp1)
v21[j] = tmp_res & 0xF
for j in range(16):
tmp = v21[j]
plain_text[j] = v22_1[v22_1[tmp]]
def encryption(plaintexts):
block_num = len(plaintexts)
for b in range(block_num):
round(plaintexts[b], b)
return plaintexts
def rev_round(cipher_text, b):
v22_1 = []
v21 = []
for i in range(16):
v22_1.append(0)
for i in range(16):
v21.append(0)
for i in range(16):
for j in range(16):
v22_1[byte_4010[j]] = plus_or_minus(shifts[b][15-i], j)
for j in range(16):
tmp = cipher_text[j]
for k in range(16):
if v22_1[k] == tmp:
tmp = k
break
for k in range(16):
if v22_1[k] == tmp:
tmp = k
break
v21[j] = tmp
for j in range(16):
res = v21[j]
tmp = keys[b][j]
v21[j] = rev_pm(res, tmp)
for j in range(16):
cipher_text[j] = v21[v22_1[j]]
def decryption(ciphertexts):
block_num = len(ciphertexts)
for b in range(block_num):
rev_round(ciphertexts[b], b)
for i in range(16):
for j in range(16):
val = plus_or_minus(i, j)
rev = rev_pm(val, j)
assert i == rev
decryption(ciphertexts)
print(ciphertexts)
for l in ciphertexts:
for i in range(8):
tmp = l[2*i] << 4
tmp += l[2*i+1]
print(chr(tmp), end='')
print()

flag: kalmar{nice!_now_please_try_the_other_two_parts}
