gooey
상위 디렉토리 - Plaid CTF 2024
문제 파일
gooey.0af9a6e6e5222e6060b651a0bc17dc4975d29e19bed8a1c69b4b644f669c8c45.tgz
친숙한 ELF x86_64 바이너리입니다. 바이너리 자체는 단순하기 때문에 분석 과정보다는 분석 결과 위주로 서술하겠습니다.
IDA 정적 분석
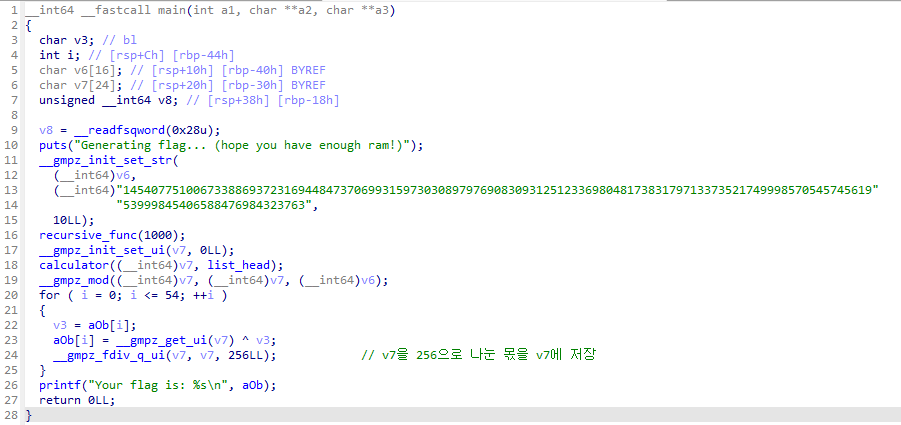
main 함수를 보면, flag를 그냥 출력해주는 프로그램이라는 것을 알 수 있습니다.
다만, 실제로 실행해보면 “hope you have enough ram!”이라는 문구처럼 말도 안되는 양의 메모리를 잡아 먹기 때문에 중간에 터집니다.
공간 최적화 + 시간 최적화를 해주어야 하는 문제입니다.
전반적으로 GNU mp bignum 모듈을 사용하고 있습니다.
위 링크에서 관련 자료들을 찾아볼 수 있습니다. bignum이 필요할 때 가장 많이 찾는 모듈이며 python 등의 타 언어에서도 해당 모듈을 사용하기 때문에 이 정도는 상식으로 알아두면 좋습니다.
main함수에서 실행되는 큰 흐름을 살펴보면
recursive_func(1000)호출로 전역변수에 있는 linked list에 엄청난 양의 node들을 할당calculator에서 생성된 linked list를 통해 특정 연산 후 연산 결과를v7에 저장v7에 있는 값을 little-endian으로 해석한 뒤aOb배열과 xor한 결과가 flag
1, 2, 3번 순서대로 분석을 해보겠습니다.
recursive_func 분석
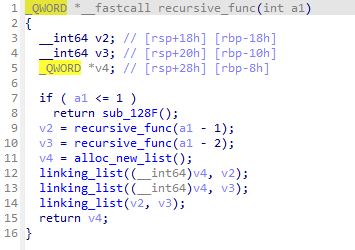
간단하지만 재귀 함수의 형식을 띄고 있습니다.
recursive_func(n)은 recursive(0) 아니면 recursive(1)이 될 때까지 recursive(n-1)과 recursive(n-2)를 호출합니다. 그리고 0 혹은 1에서는 sub_128F를 호출합니다.
먼저 함수 alloc_new_list와 linking_list를 살펴보겠습니다.
alloc_new_list- 전역변수인 linked_list head의 node를 할당 후 link합니다. 이때, node도 list의 형태입니다. list들이 서로 연결되어서 큰 list를 형성하는 구조입니다.
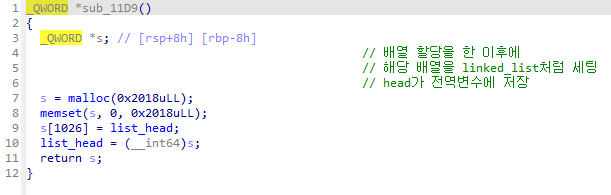
linking_list- 전역변수에 있는 큰 linked list의 노드 두 개를 인자로 받아서 노드 두 개를 link합니다. 이는 큰 linked list의 연결 관계와는 다르며, 이 연결 관계는 list 형식으로 된 node 내부의 element를 이용하여 link합니다.
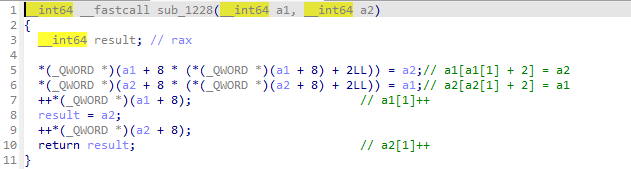
그 다음 recursive(0), recursive(1)에서 수행하는 동작인 sub_128F를 살펴보겠습니다.
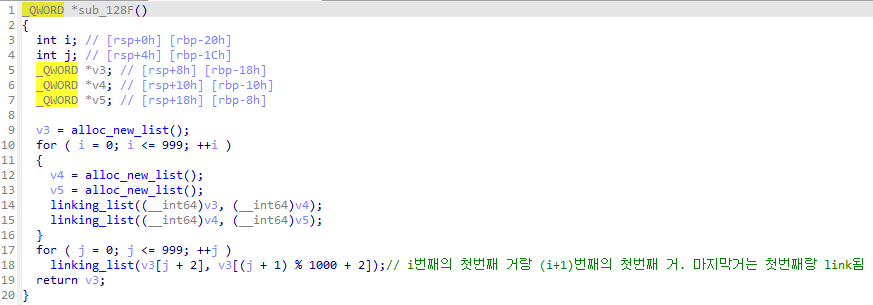
v3에 노드를 할당하고, for문을 1000번 돌면서 v4, v5에 노드 할당 후 link 작업을 수행합니다. 마지막으로 17 line부터 for문을 1000번 돌면서 link 작업을 수행합니다.
결과적으로 (1 + 2000)개의 node가 새롭게 할당되며,
2001개의 node 사이의 연결 관계는 v3은 v4_0, v4_1, … , v4_999 와 연결되어 있고,
v4_i는 v3, v4_(i-1), v4_(i+1), v5_i와 연결되어 있고,
v5_i는 v4_i와 연결되어 있는 상태가 됩니다.
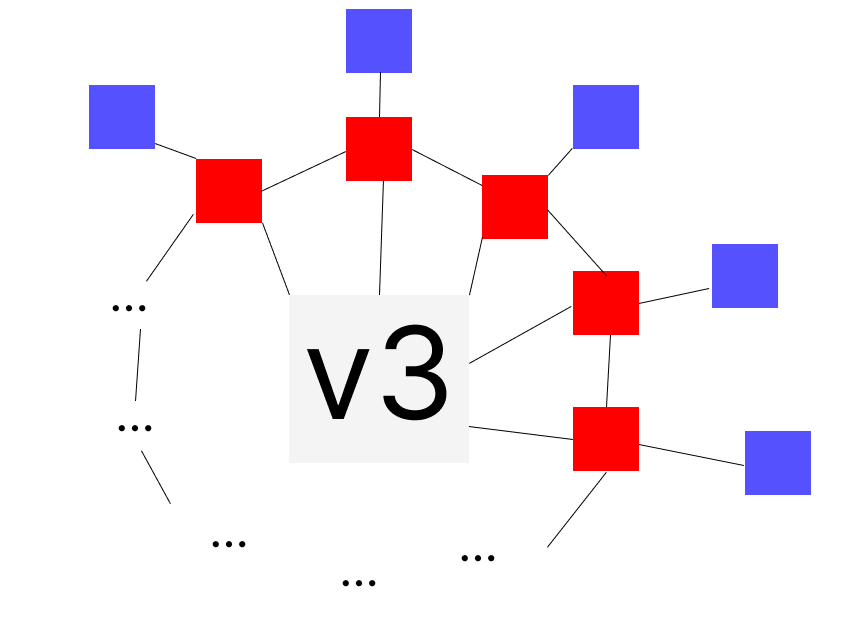
그림으로 표현하면 위와 같습니다. v4에 해당하는 빨간색 노드들이 원순열처럼 link되어 있고, 중간의 v3 노드와 link되어 있습니다. 그리고 각각의 v4 노드들은 대응하는 v5 노드와 link되어 있는 형태입니다.
이렇게 할당한 뒤 v3이 가리키는 node를 반환합니다.
그리고 recursive(n)에서는 먼저 v4에 새로운 node 할당 후 그 node와 recursive(n-1)과 recursive(n-2)를 모두 link합니다. 결과적으로는 삼각형처럼 3개가 서로 link됩니다.
그리고 v4가 가리키는 node를 반환합니다.
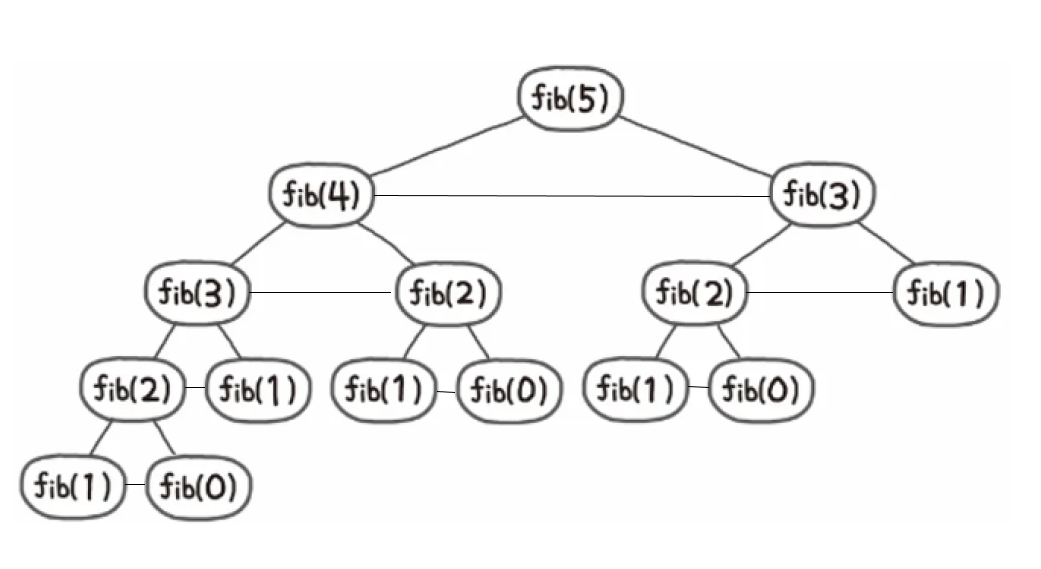
recursive()에서 반환하는 node들만 나타내보면 위 그림으로 표현할 수 있습니다.
피보나치를 재귀로 구현하였을 때 생성되는 함수 tree와 거의 유사하게 recursive가 호출되는데, 여기서 recursive(N)의 반환 node와 recursive(N-1)의 반환 node, recursive(N-2)의 반환 node가 삼각형처럼 서로 서로 link되는 형태입니다.
calculator 분석
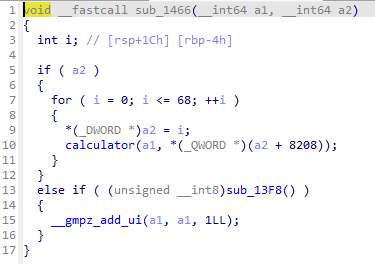
이것 또한 재귀 함수로 구현되어 있습니다.
5번 line의 if문은 전역변수의 linked list의 마지막 node가 아닌 이상 무조건 만족하게 됩니다.
그러면 head부터 순회하면서 마지막 node에 도달할 때까지 calculator가 계속 호출됩니다.
각 node마다 0~68까지의 값을 넣고 호출하며, 재귀함수이기 때문에 마지막 else if 분기로 빠지게 되는 calculator는 pow(69, [node 개수]) 만큼 호출됩니다.
else if분기에서는 sub_13F8을 호출합니다. 반환 값이 True면 main의 v7에 1을 더해줍니다.
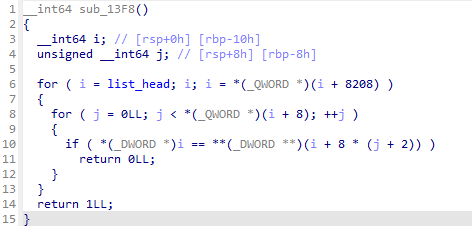
sub_13F8에서는 head부터 끝까지 linked list를 순회하면서, node와 linking_list 로 연결된 다른 node들에 해당하는 값이 본인 node의 값과 다른지 검증합니다. 이 조건이 모든 node에 대해서 만족해야 1을 return하고 아니면 0을 return합니다.
생각을 해보면 else if문으로 도달하기 까지 [node 개수] 횟수 만큼 calculator 호출하면서 각 node들에 값을 대입해 주었습니다. 그 경우의 수가 pow(69, [node 개수])가 되는 것이구요.
즉, 최종적으로 v7에 들어가게 될 값은 모든 노드에 0~68 중 하나의 값을 할당하는 pow(69, [node 개수])가지의 경우 중 각 node들의 값이 자기와 연결된 다른 node들의 값과 모두 다른 경우의 수가 됩니다.
이 경우의 수를 구하면 little-endian으로 해석한 뒤 xor 연산으로 flag를 얻어낼 수 있습니다.
수학 문제인데, 바로 옆에 ICPC finalist이신 yijw0930 가 계셔서 문제 상황 설명 드리니 10여분만에 해당 경우의 수를 구하는 솔버 코드를 뚝딱 만들어 주셨습니다.
solver.py
print('hello')
buf = [0x22, 0x4F, 0x42, 0xBA, 0x90, 0xB9, 0x2F, 0x77, 0x7C, 0xF7, 0xC1, 0x18, 0x72, 0xE9, 0x53, 0x38, 0x94, 0xC8, 0xD0, 0xAF, 0x57, 0x09, 0x2E, 0x8C, 0xE9, 0xE0, 0x1E, 0x01, 0x6B, 0x1B, 0x20, 0xA8, 0x6D, 0xEB, 0x43, 0xC1, 0x70, 0xF5, 0xA5, 0xF9, 0xBD, 0xC5, 0xC0, 0x07, 0x6D, 0x57, 0x37, 0xEE, 0x95, 0x75, 0x40, 0x7A, 0xF3, 0x8B, 0x54]
N=1454077510067338869372316944847370699315973030897976908309312512336980481738317971337352174999857054574561953999845406588476984323763
C=69
D=[0 for i in range(1005)]
D[1]=0
D[2]=(C-1)*(C-2)
for i in range(3,1001):
D[i]=D[i-1]*(C-3)+D[i-2]*(C-2)
D[i]%=N
x=pow(C-1,1000,N)
x=x*D[1000]%N
E=[0 for i in range(1005)]
E[0]=E[1]=x
for i in range(2,1001):
E[i]=E[i-1]*E[i-2]*(C-1)*(C-2)%N
res=E[999]*C%N
x = res
print(x)
for i in range(55):
buf[i] = (buf[i] ^ x) & 0xff
x //= 0x100
print(bytes(buf))
DP(Dynamic Programming)을 이용하여 경우의 수 수학 문제를 계산해주면 flag를 구할 수 있습니다.

flag: PCTF{did_you_know?_GUI_stands_for_Graph_User_Interface}
