t0y-b0x
상위 포스트 - bi0s CTF 2024
이름: 정지민
닉네임: mini_chip
소속: 고려대학교 사이버국방학과
분야: Reversing, Cryptography
체감 난이도(1~10): 5+
flag: bi0sctf{L1n34rly_Un5huffl3d_T0y5}
문제 파일
풀이 과정
랜섬웨어 유형의 문제입니다.
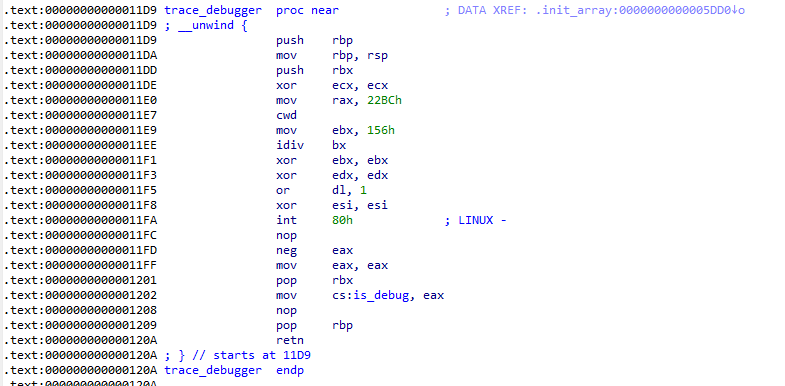
먼저 init_array에서 int 80h syscall 호출이 있습니다.
ptrace가 호출되며 그 결과값인 eax 값을 가공해서 is_debug 전역 변수에 저장합니다.
디버깅 중이면 is_debug 를 1로 set, 아니면 0으로 unset합니다.
이 안티 디버깅 로직을 해석하지 못하면, 역연산이 불가능한 문제로 변모해 버립니다.
디버깅 여부에 따라서(is_debug 변수의 여부에 따라) s-box 로직이 추가되는 구조를 띄고 있습니다. 이와 관련된 자세한 내용은 후술하겠습니다.
main function

메인 함수 자체는 간단한 편에 속합니다.
로직은 전반적으로 AES와 유사한 방식으로 구현되어 있습니다.
calc_16byte 함수는 key expansion과 관련한 로직입니다.
그리고 70 line의 encryptor 함수가 S-box가 다른 선형구조의 로직으로 대체된 형태의 AES 암호의 형태를 띄고 있습니다. 그리고 운영 모드는 ECB모드로 block들 사이에서는 아무런 영향을 주고 받지 않습니다.
그리고 46~51 line에서 안티 디버깅 로직이 구현되어 있는데, is_debug 변수값의 set 여부에 따라 box_int를 새롭게 초기화합니다.
기존에 box_int는 0~255까지의 값이 저장되어 있는 int 배열이었습니다.

그렇기 때문에 위 함수를 보면 S-box와 관련된 로직임을 알 수 있지만, 실제로는 아무런 동작을 수행하지 않는 null_sub()가 되게 됩니다.
하지만, 디버깅 환경에서 is_debug 변수가 set되어서 46~51 line의 if문이 실행되게 된다면,
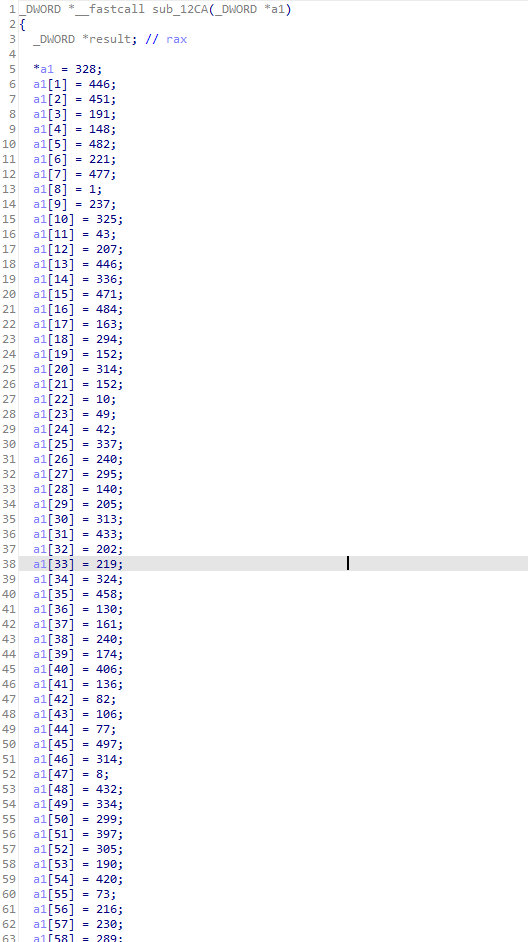
이런 식으로 s-box가 초기화되게 됩니다. 그럼 아까 null_sub()처럼 동작하던 함수가 더 이상 null_sub가 아닌 실제 s-box 치환 로직으로 작동하게 되면서 암호가 비선형적으로 바뀌게 되는 것이죠.
그 외에 선형적인 형태의 로직이 추가되었습니다. 디버깅이 아닌 실제 환경에서 s-box 치환을 대신할 로직으로 사용된 것 같습니다.
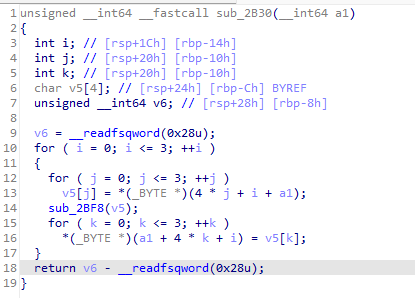

솔직히 선형적이라는 것 말고는 로직 자체에 특수한 의미를 부여하지는 못했습니다. 그래서 구현도 그냥 C코드에 적힌 그대로 구현하였습니다.
implement.py
import copy
byte_box = [
0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B,
0x36, 0x6C, 0xD8, 0xAB, 0x4D, 0x9A, 0x2F, 0x5E, 0xBC, 0x63,
0xC6, 0x97, 0x35, 0x6A, 0xD4, 0xB3, 0x7D, 0xFA, 0xEF, 0xC5,
0x91, 0x39
]
init_buf = "abcdef0123456789"
init_list = []
for i in init_buf:
init_list.append(ord(i))
def sub_27E7(dst, src):
for i in range(16):
dst.append(src[i])
v8 = 16
a4 = 176
v9 = 1
while (v8 < a4):
tmp = []
for i in range(4):
tmp.append(dst[v8 - 4 + i])
if not (v8 % 16):
tmp_cnt = v9
v9 += 1
tmp[0] = byte_box[tmp_cnt]
tmp[1] = 0
tmp[2] = 0
tmp[3] = 0
for i in range(4):
res = tmp[i] ^ dst[v8 - 16]
dst.append(res)
v8 += 1
return dst
def sub_22EB():
src = "[yb2zg5w7k|yiyi$"
res = []
for i in src:
res.append(ord(i))
res.append(15)
for i in range(len(res)):
res[i] ^= (i+15)
print(res)
return res
dst = []
print([hex(elem) for elem in sub_27E7(dst, init_list)])
for i in sub_22EB():
print(chr(i), end='')
print()
def transpose(src):
dst = []
for i in range(4):
for j in range(4):
dst.append(src[4*j + i])
return dst
def xor_func(dst, src):
for i in range(16):
dst[i] ^= src[i]
def shift_rows(dst):
for i in range(4):
cnt = 0
while cnt < i:
tmp = dst[4*i]
for j in range(3):
dst[4*i+j] = dst[4*i+1+j]
dst[4*i+3] = tmp
cnt +=1
def sub_2AD6(a1, a2):
res = 0
for i in range(8):
if (a2 & 1) != 0:
res ^= a1
tmp = a1 & 0x80
a1 <<= 1
a1 &= 0xff
if (tmp == 0x80):
a1 ^= 0x1B
a2 >>= 1
return res
def sub_2BF8(dst):
tmp = copy.deepcopy(dst)
print(tmp)
a1 = sub_2AD6(tmp[0], 2) ^ sub_2AD6(tmp[1], 3) ^ sub_2AD6(tmp[2], 1) ^ sub_2AD6(tmp[3], 1)
dst[0] = a1
a2 = sub_2AD6(tmp[0], 1) ^ sub_2AD6(tmp[1], 2) ^ sub_2AD6(tmp[2], 3) ^ sub_2AD6(tmp[3], 1)
dst[1] = a2
a3 = sub_2AD6(tmp[0], 1) ^ sub_2AD6(tmp[1], 1) ^ sub_2AD6(tmp[2], 2) ^ sub_2AD6(tmp[3], 3)
dst[2] = a3
a4 = sub_2AD6(tmp[0], 3) ^ sub_2AD6(tmp[1], 1) ^ sub_2AD6(tmp[2], 1) ^ sub_2AD6(tmp[3], 2)
dst[3] = a4
def sub_2B30(dst):
for i in range(4):
tmp = []
for j in range(4):
tmp.append(dst[j*4+i])
sub_2BF8(tmp)
for k in range(4):
dst[i+4*k] = tmp[k]
print(dst)
#transposed -> pad("Tis is a secret:" + %1024)의 transpose
#init_16byte -> sub_27E7(%16s)의 결과물
def encryptor(transposed, init_16byte):
tmp = []
for i in range(16):
tmp.append(0)
#first round
tmp = transpose(init_16byte[0:16])
print(tmp)
xor_func(transposed, tmp)
print(transposed)
#mid round
for rnd in range(9):
tmp = transpose(init_16byte[16*(rnd+1):16*(rnd+2)])
shift_rows(transposed)
if rnd == 0:
print(transposed)
sub_2B30(transposed)
xor_func(transposed, tmp)
#final round
tmp = transpose(init_16byte[160:176])
shift_rows(transposed)
xor_func(transposed, tmp)
flag = "몰라..ㅋㅋㅋ"
init_16byte = "0123456789abcdef"
init_list = []
for i in init_16byte:
init_list.append(ord(i))
init_16byte = sub_27E7([], init_list)
key = [84, 105, 115, 32, 105, 115, 32, 97, 32, 115, 101, 99, 114, 101, 116, 58, 16]
#padding(key + list(flag)) 16바이트 단위로 맞춰준다~
#이후에 16바이트가 한 블럭으로 해서 block이라 하자
block = (key+list(flag))[0:16] #key 길이가 17이니까 사실 block은 key[0:16]이겠지??
print(block)
block = (transpose(block))
#blcok을 아니까 여기서 init_16byte를 구하는 거일듯
encryptor(block, init_16byte)
print(block)
'''
encrypted = "62dab26a74a375d01402ada3879a4031" #그냥 저대로 hex값임 [0x62, 0xda, ...]
#이후에 block들도 encrypt하는데 여기서 flag 구하는거일듯요
encryptor(block, init_16byte)
'''
print(sub_2AD6(0x64, 2))
print(sub_2AD6(0x5C, 1) ^ 200)
역산은 soon_haari(god_haari)가 진행하여 flag를 구해주었습니다. 블록 암호 선형 분석을 위하여 129개의 원하는 평문에 대한 암호문 값을 요구했기에 이를 뽑아주는 gdb script를 작성하여 데이터를 뽑았습니다.
gdbscript.py
#gdb -q -x gdbscript.py
import gdb
import re
byte_box = [
0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B,
0x36, 0x6C, 0xD8, 0xAB, 0x4D, 0x9A, 0x2F, 0x5E, 0xBC, 0x63,
0xC6, 0x97, 0x35, 0x6A, 0xD4, 0xB3, 0x7D, 0xFA, 0xEF, 0xC5,
0x91, 0x39
]
init_buf = "abcdef0123456789"
init_list = []
for i in init_buf:
init_list.append(ord(i))
def sub_27E7(dst, src):
for i in range(16):
dst.append(src[i])
v8 = 16
a4 = 176
v9 = 1
while (v8 < a4):
tmp = []
for i in range(4):
tmp.append(dst[v8 - 4 + i])
if not (v8 % 16):
tmp_cnt = v9
v9 += 1
tmp[0] = byte_box[tmp_cnt]
tmp[1] = 0
tmp[2] = 0
tmp[3] = 0
for i in range(4):
res = tmp[i] ^ dst[v8 - 16]
dst.append(res)
v8 += 1
return dst
key = sub_27E7([], init_list)
gdb.execute("file ./fordebug")
base = 0x555555554000
breakpoint = [0x0000000000002643]
gdb.execute("b*"+hex(base+breakpoint[0]))
def set_val(val0, val1):
gdb.execute("set *(long long*)($rbp-0x860) = %d"%val0)
gdb.execute("set *(long long*)($rbp-0x858) = %d"%val1)
gdb.execute("x/16b $rbp-0x860")
gdb.execute("x/2gx $rbp-0x860")
f = open("result.txt", "w")
def bit2byte(l):
res = 0
ll = []
for i in range(8):
for j in range(8):
ll.append(l[8*i+7-j])
for i in range(len(l)):
res |= (1 << i) * ll[63 - i]
return res
for i in range(129):
gdb.execute("run "+"<<<"+"".join(init_buf+"\n"), to_string = True)
val0 = 0
val1 = 0
tmp = []
for j in range(128):
tmp.append(0)
if i > 0:
tmp[128-i] = 1
val0 = bit2byte(tmp[0:64])
val1 = bit2byte(tmp[64:])
set_val(val0, val1)
gdb.execute("ni")
f.write(val0.to_bytes(8, byteorder="big").hex()+val1.to_bytes(8, byteorder="big").hex()+"\n")
values = gdb.execute("x/2gx $rbp-0x850", to_string=True)
print(type(re.findall("0x([0-9a-f]+)", values)[1]))
print(re.findall("0x([0-9a-f]+)", values)[2])
f.write(int(re.findall("0x([0-9a-f]+)", values)[1], 16).to_bytes(8, byteorder="little").hex() + "\n")
f.write(int(re.findall("0x([0-9a-f]+)", values)[2], 16).to_bytes(8, byteorder="little").hex() + "\n")
f.write("\n")
f.close()
여기서 제가 좀 실수를 해서 데이터 뽑는 데 순서가 살짝 잘못되어버린 참사가 일어났지만, 다행히 순하리가 잘 수습하여 플래그를 추출하는 데 성공했습니다.
리틀 엔디안으로 인해 순서가 뒤집히는 것은 byte 단위입니다. 8bit 단위로 뒤집히기 때문에 16byte인 128bit를 통째로 거꾸로 뒤집는다고 해서 리틀엔디안으로 바뀌는 것이 아닙니다. 굉장히 기초적인 지식인데 실수를 저질러버렸네요. 그래도 풀어서 다행입니다.
바톤터치했다. 나다.
지민이형이 잘 포팅해준 implement.py를 살펴보면 AES 암호체계를 닮았다는 생각을 충분히 할 수 있다. 그런데 중간에 끼어 있는 함수가 조금 이상하다.
for rnd in range(9):
tmp = transpose(init_16byte[16*(rnd+1):16*(rnd+2)])
shift_rows(transposed)
if rnd == 0:
print(transposed)
sub_2B30(transposed)
xor_func(transposed, tmp)
원래같으면 암호의 혼돈성을 담당하는 SubBytes, MixColumn이 들어가야 할 자리에 SBox는 어디가고 다음과 같은 게 놓여 있다.
def sub_2AD6(a1, a2):
res = 0
for i in range(8):
if (a2 & 1) != 0:
res ^= a1
tmp = a1 & 0x80
a1 <<= 1
a1 &= 0xff
if (tmp == 0x80):
a1 ^= 0x1B
a2 >>= 1
return res
def sub_2BF8(dst):
tmp = copy.deepcopy(dst)
print(tmp)
a1 = sub_2AD6(tmp[0], 2) ^ sub_2AD6(tmp[1], 3) ^ sub_2AD6(tmp[2], 1) ^ sub_2AD6(tmp[3], 1)
dst[0] = a1
a2 = sub_2AD6(tmp[0], 1) ^ sub_2AD6(tmp[1], 2) ^ sub_2AD6(tmp[2], 3) ^ sub_2AD6(tmp[3], 1)
dst[1] = a2
a3 = sub_2AD6(tmp[0], 1) ^ sub_2AD6(tmp[1], 1) ^ sub_2AD6(tmp[2], 2) ^ sub_2AD6(tmp[3], 3)
dst[2] = a3
a4 = sub_2AD6(tmp[0], 3) ^ sub_2AD6(tmp[1], 1) ^ sub_2AD6(tmp[2], 1) ^ sub_2AD6(tmp[3], 2)
dst[3] = a4
def sub_2B30(dst):
for i in range(4):
tmp = []
for j in range(4):
tmp.append(dst[j*4+i])
sub_2BF8(tmp)
for k in range(4):
dst[i+4*k] = tmp[k]
print(dst)
대충 봐보면 sub_2AD6 는 GCM에서 사용하는 것과 비슷한 $\mathbb{F}_{2^{8}}$의 갈루아 필드 연산을 하고 있고, sub_2BF8 는 그걸 바탕으로 또 무슨 MixColumn 비스무리한 연산을 하고 있고, sub_2B30 는 최종적으로 그걸 4번 하는 것처럼 보인다. 디테일한건 중요치 않다. 여기서 중요한 것은 모든 연산들이 xor, shift, mask밖에 없다는 것이다. 그래서 이 암호는 모든 것이 선형적이다.
지민이형이 땀을 뻘뻘 흘리며 implement.py를 틀린 부분이 있는지 검사하고 있길래, 분석을 마친 나는 자신있게 말했다. 아무 키, 대신 같은 키로 평문-암호문쌍 129개만 좀 구해달라고.
암호가 선형적이게 되면 Affine 성질을 만족하게 된다. 공부해보길 바란다.
\[enc(A \oplus B) + enc(0) = enc(A) \oplus enc(B)\]남은 주어진 문제는 평문의 1블록, 암호문 4블록이 알려져 있어, 나머지 평문 3블록을 구하는 것이 목적이고, 이는 손쉽게 선형대수학의 힘을 빌려 가능하다.
output.txt는 지민이형이 gdbscript를 이용해 뽑아준 129개의 평암호문쌍이다.
output.txt
00000000000000000000000000000000
60af7c7a17d4b49e
a9bad7c39f460ea3
00000000000000000000000000000001
60af7d7a17d5b49e
abbad7c39f460ea0
00000000000000000000000000000002
60af7e7a17d6b49e
adbad7c39f460ea5
00000000000000000000000000000004
60af787a17d0b49e
a1bad7c39f460eaf
...
ex.sage
pt = pt[:8][::-1] + pt[8:][::-1] 이걸 게싱하는게 말이 되나 ㅋㅋㅋ
그래도 데이터 잘 뽑아준 지민이형에게 이 문제를 바친다.
from impl import encryptor, xor
import os
res = open("output.txt", "r").read().split("\n")
cts = {}
for i in range(129):
'''
st = res[4 * i].split(" ")
aa, bb = int(st[0], 16), int(st[1], 16)
aa = int(aa).to_bytes(8, "little")
bb = int(bb).to_bytes(8, "little")
pt = aa + bb
'''
pt = bytes.fromhex(res[4 * i])
pt = pt[:8][::-1] + pt[8:][::-1]
a = res[4 * i + 1]
b = res[4 * i + 2]
ct = bytes.fromhex(a + b)
cts[pt] = ct
zero = cts[bytes(16)]
M = Matrix(GF(2), 128, 128)
for i in range(128):
pt = int(2^i).to_bytes(16, "big")
# print(pt)
ct = cts[pt]
ct = bytes(xor(zero, ct))
ct = int.from_bytes(ct, "big")
for j in range(128):
M[j, i] = (ct >> j) & 1
M_inv = M^-1
ct = "62dab26a74a375d01402ada3879a4031d8a485ec177380f44ca4ab9441545999003a8070e7eacd6ceabbf280d53859e278e7bc0e69b3f60de7493b510088dc8b"
ct = bytes.fromhex(ct)
assert len(ct) == 64
key = [84, 105, 115, 32, 105, 115, 32, 97, 32, 115, 101, 99, 114, 101, 116, 58]
def enc(c):
c = int.from_bytes(c, "big")
c = [(c >> j) & 1 for j in range(128)]
c = vector(GF(2), c)
p = M * c
pp = 0
for i in range(128):
pp += ZZ(p[i]) << i
return int(pp).to_bytes(16, "big")
def dec(c):
c = int.from_bytes(c, "big")
c = [(c >> j) & 1 for j in range(128)]
c = vector(GF(2), c)
p = M_inv * c
pp = 0
for i in range(128):
pp += ZZ(p[i]) << i
return int(pp).to_bytes(16, "big")
p = bytes(16)
c = cts[p]
assert c == bytes(xor(zero, enc(p)))
for p in cts:
c = cts[p]
assert c == bytes(xor(zero, enc(p)))
zero = dec(zero)
for p in cts:
c = cts[p]
assert p == bytes(xor(zero, dec(c)))
toxor = xor(dec(ct[:16]), key)
# print(toxor)
flag = b""
for i in range(4):
c = ct[16 * i:16 * (i + 1)]
p = xor(toxor, dec(c))
p = bytes(p)
print(p)
flag += p
print(flag.decode())
b'Tis is a secret:'
b'\x10bi0sctf{L1n34rl'
b'y_Un5huffl3d_T0y'
b'5}\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e\x0e'
Tis is a secret:bi0sctf{L1n34rly_Un5huffl3d_T0y5}
